Ontstaan van de ƒ-waarden

De opening van een lens geeft aan hoeveel licht er door de lens doorgelaten wordt. We leggen hier uit hoe men aan het begrip ƒ-waarde gekomen is.

De algemene pagina over de opening is hier. Lees ook de informatie over het onstaan van de lenzen (historisch overzicht van enkelvoudige lens tot de meest complexe systemen zoals wij die nu kennen).

Vroeger werden fototoestellen uitgerust met verwisselbare lenzen (dit is nog altijd het geval voor de betere toestellen). Men moest een manier vinden om een correcte belichting te bekomen ongeacht de gebruikte lens. De belichting hangt af van twee parameters, namelijk

• de sluitertijd (hoe lang de gevoelige laag belicht wordt, dit is onafhankelijk van de lens), en
• de lichtsterkte van de lens. De lichtsterkte geeft aan hoeveel licht er op iedere vierkante mm van de film valt.

Na een aantal berekeningen kwam men tot de conclusie dat de hoeveelheid licht per vierkante mm pellicule enkel afhankelijk was van de grootte van de lens (diameter, die men dan kunstmatig kon verkleinen door een diafragma te gebruiken) en de brandpuntafstand. Een lens met een lange brandpuntafstand (een tele-lens) heeft proportioneel een grotere objectieflens nodig om de film even sterk te belichten.

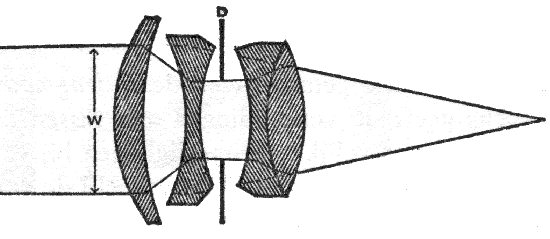
Om het exact voor te stellen gebruikt men niet de diamater van het diafragma (D), maar zijn projectie, de intredepupil (W), die door de concentrerende werking van de lenzen bepaalt hoeveel licht de lens opvangt.

En zo is de diafragma-waarde ontstaan zoals wij die nu kennen: een verhouding van de brandpuntafstand tot de diafragma-opening (eigenlijk intredepupil). Daarom wordt de diafragma-waarde ook altijd uitgedrukt als een breukdeel. Met een lens met een diafragma-waarde van "1/4" valt er altijd evenveel licht op de film; je kan dus lenzen verwisselen zonder rekening te moeten houden met de effectieve opening in mm of inch: de fabrikant heeft het al voor jou uitgerekend en op de diafragma-ring gedrukt.

De "ƒ" komt van "distance focale" of brandpuntafstand (men gebruikt een cursieve ƒ en geen gewone f). Het is altijd een kleine ƒ en heeft niets te maken met facebook. De grote F geeft het brandpunt aan (Foyer).

Omdat er licht verloren gaat in het lenzensysteem is de effektieve ƒ-waarde kleiner dan de berekende ƒ-waarde. De optieken die in filmtoestellen gebruikt worden hebben een aanduiding van de effektieve ƒ-waarde, om belichtingsverschillen tussen scènes te voorkomen (als er van lens gewisseld moet worden). Dit heet de τ-waarde (van transmittance).

Is ƒ/2.8 altijd even lichtsterk?

Maar bij kleinere filmformaten kan men ook kleinere lenzen gebruiken: de te belichten oppervlakte is namelijk kleiner. Een ƒ/2.8 lens voor een pocket instamatic is kleiner dan een ƒ/2.8 lens voor een kleinbeeld toestel. Het is belangrijk te weten dat er op iedere vierkante mm van de film evenveel licht valt.

Maar er is een verschil met de digitale wereld. In de praktijk bedraagt de sensorafmeting van een compact fototoestel 2.7×3.6mm, daar waar een reflex met een sensor van 24×36mm werkt. Als de lens een opening van ƒ/2.8 heeft, dan zal er op ieder vierkante mm van beide sensoren evenveel licht vallen. Maar de sensor van het compact toestel heeft meer pixels per vierkante mm, en heeft dus meer licht nodig om iedere pixel van voldoende licht te voorzien. Een ƒ-waarde van ƒ/2.8 die toereikend was voor een reflexsensor, is dat niet meer voor een compact sensor. Met zijn kleine pixels (100× kleiner dan die van een spiegelreflex) heeft de compact 100 keer meer licht nodig per vierkante mm. Zo'n hoge belichting is technisch niet haalbaar (men zou ƒ-waarden van 0.3 moeten halen), daarom bevat het beeld van een compact fototoestel altijd meer ruis.

Relatieve waarde

Het diafragma van deze lens gaat van 16 tot 1.8
Maar waarom deze vreemde getallen?

Het diafragma van deze lens gaat van 2.8 tot 22
Is deze lens lichtsterker dan de vorige?

Paginas die volgens Google je zouden kunnen interesseren